Fig. 3 below gives examples for graphite [5]. The black band structure is the one calculated with a complete basis set, consisting of the C s, p, and d NMTOs with the three energies (N=2) indicated in black in the top picture. Fig. 3a shows the downfolded C pz NMTO obtained by downfolding all partial waves except C pz, and using an energy mesh (red) in the range of the C 2pz bands. The basis set consisting of this pz orbital placed on any C-site, yields the top red bands. These are indistinguishable from the correct, black bands except where additional bands cross. The C pz NMTO is localized by the requirement that its pz character vanishes on all other C-sites. Figs. 3b and 3c demonstrate that we can also pick merely the Π -bonding or the Π *-antibonding bands. In these cases, the basis consists of a C pz NMTO on every second site; the pz waves on the neighboring three sites are now downfolded, and depending on whether the energy mesh is chosen in the region of the Π - or the Π * -bands, the method picks the orbital which bonds or antibonds to its neighbors. Fig. 3d shows one of the three sp2 σ -bond orbitals and the corresponding three σ -bands.
In order to pick a particular set of bands, the NMTO set must contain as many orbitals as there are bands to be picked, and the orbitals must be chosen with appropriate characters. For an isolated set of bands, such an NMTO set converges to the exact Hilbert space as the energy mesh spans the bandwidth finer and finer. After symmetrical orthonormalization, such a truly minimal NMTO set therefore constitutes a set of atom-centered Wannier functions. The NMTO downfolding method thus allows for direct generation, as opposed to projection, of Wannier functions.
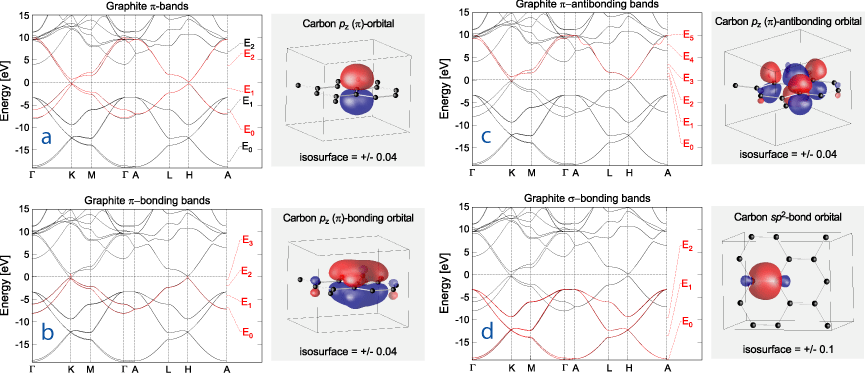
Fig. 3. Black: Band structure of graphite. Red: Bands obtained using downfolded NMTOs. The latter are shown as contours, with red/blue labelling the sign.
Currently, we are working on using NMTO Wannier-like functions to unravel the bonding in intermetallic systems, study metals under pressure, and visualize the occupied states in SWNTs. In the latter case, these orbitals may be useful in explaining the trends of the NMR chemical shifts.
[1] Andersen, O.K; Saha-Dasgupta. T. Phys. Rev. B, 2000, 62, R16219.
[2] Andersen, O.K.; Saha-Dasgupta, T.; Tank, R.W.; Arcangeli, C.; Jepsen, O.; Krier, G. Lecture Notes in Physics, 2000, 535, 3.
[3] Andersen, O.K.; Saha-Dasgupta, T.; Ezhov, S.; Tsetseris, L.; Jepsen, O.; Tank, R.W.; Arcangeli, C.; Krier, G. Psi-k Newsletter, 2001, 45, 86.
[4] Andersen, O.K.; Saha-Dasgupta, T.; Ezhov, S. Bulletin of Materials Science, 2003, 26, 19.
[5] Zurek, E.; Jepsen, O.; Andersen, O.K. ChemPhysChem, 2005, 6, 1934.