Max-Planck-Institut FKF, Stuttgart, D-70569, Germany
The TB-LMTO-ASA method is reviewed and generalized to an accurate and robust TB-NMTO minimal-basis method, which solves Schrodinger's equation to Nth order in the energy expansion for an overlapping MT-potential, and which may include any degree of downfolding. For N = 1, the simple TB-LMTO-ASA formalism is preserved. For a discrete energy mesh, the NMTO basis set may be given as:
,
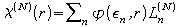
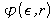evaluated on the mesh, 
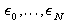. This basis
solves Schrodinger's equation for the MT-potential to within an error proportional
to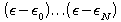 
. The Lagrange matrix-coefficients, 
,
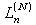as well as the Hamiltonian and overlap matrices for the NMTO set, have
simple expressions in terms of energy derivatives on the mesh of the Green
matrix, defined as the inverse of the screened KKR matrix. The variationally
determined single-electron energies have errors proportional to 
.
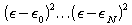A method for obtaining orthonormal NMTO sets is given and several applications
are presented.
A reprint of this paper can be obtained from cond-mat in Germany
or in the US
Electronic Structure and Physical Properties of Solids. The Uses of the LMTO Method, ed. H. Dreyssé. Berlin/Heidelberg: Springer (2000). Lect. Notes Phys., 535 3-84, 2000.
Max-Planck Institut für Festkörperforschung;
Postfach 80 06 65 D-70506 Stuttgart
