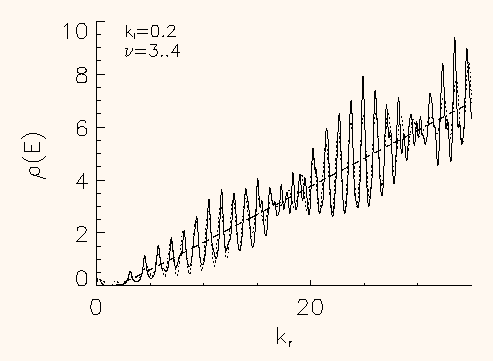
Abbildung 1: Lorentz-geglättete Zustandsdichte einer sphärischen
Kavität. Die durchgezogene Linie wurde aus dem quantenmechanischen
Spektrum bestimmt, die gebrochenen Kurve zeigt eine semiklassische Näherung.
| Max-Planck-Institut für Festkörperforschung | ||||
| Andersen Group | LMTO | C60 | GW | Clusters |
Es gilt daher, neue Methoden zu erproben, die in der Lage sind, die spezifischen Eigenschaften mesoskopischer Systeme zu erfassen, ohne detaillierte Informationen über die mikroskopische Struktur zu benötigen. Zu diesem Zwecke sucht man sich natürlich möglichst einfache Systeme, bei denen die interessierenden Effekte praktisch in Reinkultur auftreten. Interessiert man sich etwa für die elektronische Struktur, so bieten sich Cluster einfacher Metalle als ideale Testobjekte an: In solchen Systemen sollte das Potential, in dem sich die Valenzelektronen bewegen, nur wenig von der Anordnung der Atome abhängen. Man wird so zum Jellium-Modell geführt, das es erlaubt, die atomare Struktur praktisch völlig zu vernachlässigen, um sich auf Effekte der endlichen Größe des Systems zu konzentrieren.
Ein interessanter mesoskopischer Effekt zeigt sich etwa in der (geeignet geglätteten) Zustandsdichte einer sphärischen Kavität wie sie in Abbildung 1 dargestellt ist. Man findet eine regelmäßige Oszillation, deren Amplitude wie bei einer Schwebung moduliert ist. Eine Oszillation in der Zustandsdichte rührt natürlich daher, daß sich die Energieniveaus des Systems zu Gruppen, den sogenannten Schalen anordnen. Die schwebungsartige Modulation bezeichnet man als Superschalen-Struktur.
Fermionische Schalen sind aus dem Atombau (Periodensystem) sowie der Kernphysik (magische Kerne) bekannt. Aber erst in mesoskopischen Systemen rücken die Energieniveaus so nahe zusammen -- ohne jedoch, wie im makroskopischen System, zu einem Kontinuum zu verschmelzen --, daß auch die Superschalen beobachtbar werden. So zeigen sich in den Massenspektren heißer Metallcluster Schwebungsmuster, die sich auf Oszillationen in der Stabilität der Cluster als Funktion ihrer Größe zurückführen lassen, welche wiederum mit Oszillationen der elektronischen Zustandsdichte zusammenhängen. Dementsprechend nennt man auch die Schwebungen in den Massenspektren Superschalen, die Oszillationen selbst Schalen und die Zahl von Valenzelektronen in besonders stabilen Clustern magische Zahlen.

Abbildung 1: Lorentz-geglättete Zustandsdichte einer sphärischen
Kavität. Die durchgezogene Linie wurde aus dem quantenmechanischen
Spektrum bestimmt, die gebrochenen Kurve zeigt eine semiklassische Näherung.
Wie Abbildung 1 zeigt, läßt sich die geglättete Zustandsdichte der sphärischen Kavität recht gut semiklassisch beschreiben. Ein besonderer Vorzug der semiklassischen Behandlung ist, daß die Zustandsdichte dabei auf natürliche Weise in einen glatten sowie einen oszillierenden Anteil zerfällt: \rho(E) dE = ( \bar \rho(E) + \tilde \rho(E) ) dE. Damit werden die interessierenden Oszillationen \tilde \rho einer direkten Untersuchung zugänglich, ohne vom viel größeren "Untergrund" \bar \rho überdeckt zu werden. Zudem erscheint in Anbetracht ihrer typischen Größe die Semiklassik als die Methode der Wahl zur Behandlung von Elektronen in Metallclustern. Nun stellt jedoch das Fermi-Gas in einer sphärischen Kavität nur ein äußerst grobes Modell der Valenzelektronen in einem Metallcluster dar. Insbesondere ist damit die Materialabhängigkeit von Schalen und Superschalen nicht zu verstehen. Das wiederum kann die Beschreibung im Rahmen selbstkonsistenter Jellium-Modelle leisten. Sie liefern allerdings nur die Gesamtenergie E(N) der Cluster als Funktion ihrer Größe, aus der man den oszillierenden Anteil numerisch extrahieren muß. Dabei geht aber die physikalische Anschauung, welche die Semiklassik bietet, verloren.
In der vorliegenden Arbeit unternehmen wir es, die Verbindung zwischen selbstkonsistenten Rechnungen im Jellium-Modell und der semiklassischen Behandlung derselben Systeme -- in Anlehnung an den idealisierten Fall der sphärischen Kavität -- herzustellen: Dazu analysieren wir zunächst, wie sich die Materialabhängigkeit im Jellium-Modell bemerkbar macht. Anschießend implementieren wir die relevanten Größen in einer semiklassischen Entwicklung.
Im einzelnen gliedert sich die Arbeit wie folgt:
| MPI-FKF | Andersen Group | Erik Koch (
koch@and.mpi-stuttgart.mpg.de)
Max-Planck-Institut für Festkörperforschung Heisenbergstraße 1 D-70569 Stuttgart |